Promise of Relevant Search Results: Vector Databases

Search fields are a near ubiquitous part of most websites these days, but have you ever felt like most times you search for something, you get irrelevant results? Most search engines used by websites are full-text search engines of varying complexity. These engines take text search input and match it against data stored in the database through the use of queries. These find data with specific queries, but what if the query is vague or in natural language?

Like regular databases, vector databases store data. What sets them apart is that they can also store the vector representations of this data. Searching or querying this data is a matter of mathematical functions instead of complex queries.

The vectors represent different properties of the data, known as 'features'. These are features can be calculated using feature extraction models. These process the documents in the database word-by-word and extract the features of the text which are common denominators. After these, the entire database can be processed again to be turned into vectorized values.

Why do this?
Vectorized values & a large set of features allow for something very useful: searching by relevancy. Any search input to such a database can be turned into vectors and then these vectors can be compared against those contained in the database. The closes values will represent the most relevant matches in the database. Since the stored data is broken up & turned into vectors on a per word basis, a sentence & it's semantic meaning can be represented as vector values.

What are vectors?
Before diving into the query process, it's crucial to understand what vectors are. A vector is a geometric concept, representing direction and magnitude. They are defined by a start point, an end point, as well as direction. They are used to represent speed, force, and many other concepts in mathematics and physics. In our case they represent how strongly relevant or irrelevant a certain 'feature' of a given 'token' is.

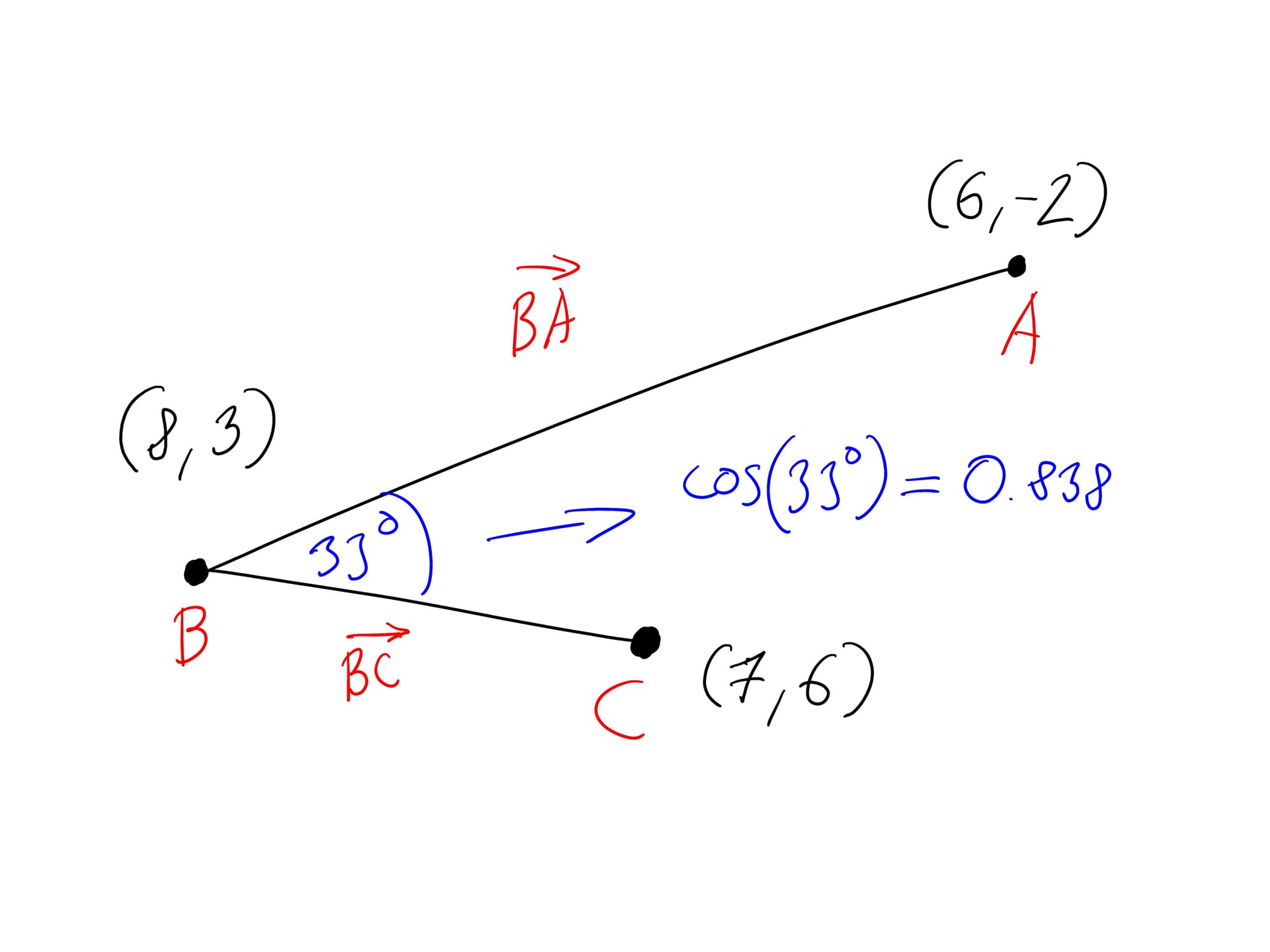
Visually a vector might be represented in 2D space as two points with coordinates (x, y), with a line between them. Note that the direction of the vector (in this case from A to B) is also a relevant factor, since in our case it would make the difference between relevant or irrelevant information.

Processing data into vectors

How does a vector database deal with data? When inputting data into a vector database, it's in human readable format. Think products or recipes that need to be processed. Before this data is query-able, it needs to go through processing consisting of 3 main steps.

1.: Tokenization
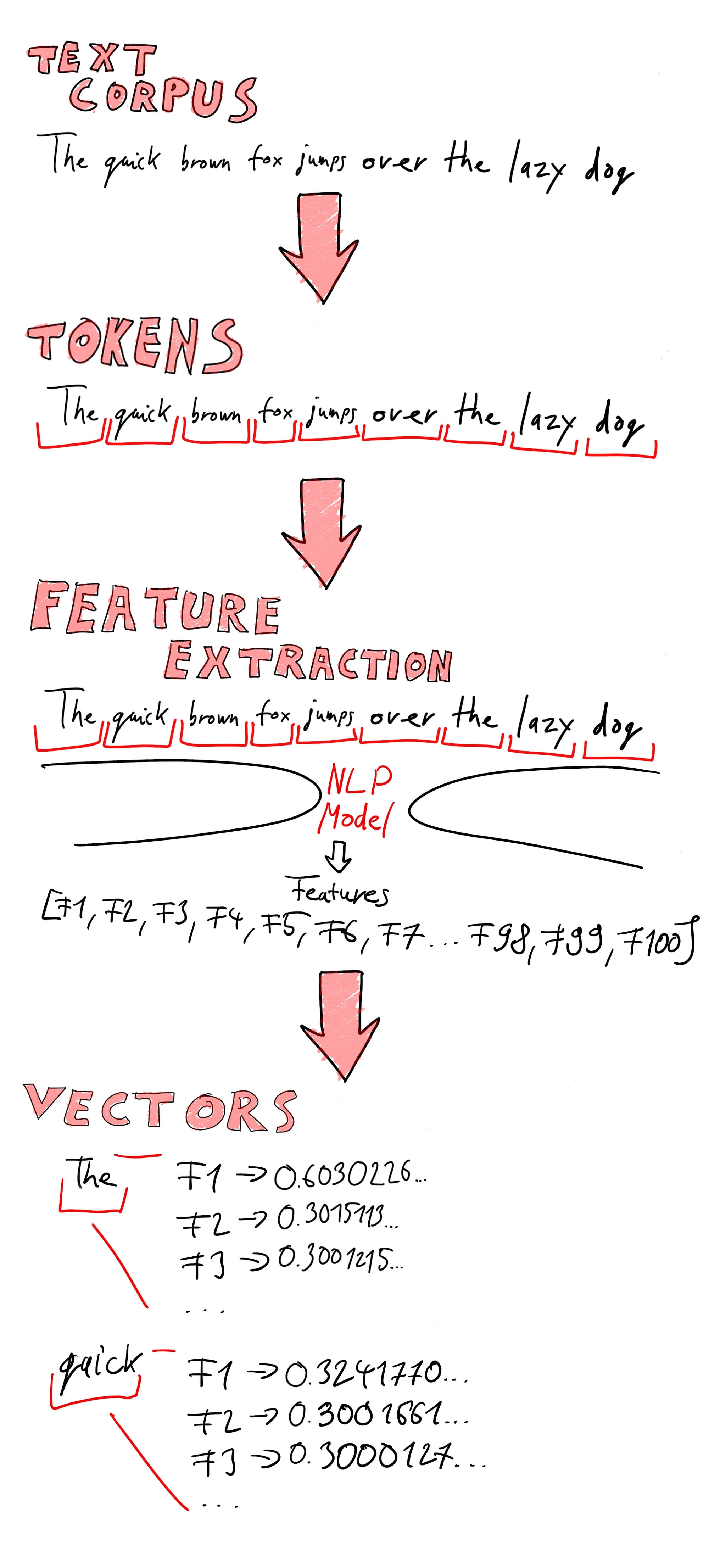
During tokenization, the input documents (text corpus or text corpora for plural) are turned into tokens, which are the component words and phrases. For example, when the sentence "The quick brown fox jumps over the lazy dog" is tokenized, the tokens will be 'The', 'quick', 'brown', 'fox', 'jumps', 'over', 'the', 'lazy', 'dog'.

2.: Feature Extraction
After the input is turned into a collection of tokens, the process of feature extraction can start. During feature extraction, a fixed set of shared features is identified in the database documents. These features can be imaged as columns in a table, which the subsequent vectorization process will create values for. There are several existing models which can prepare the features, such as Bag of Words, TF-IDF, Word2Vec.

3.: Vectorization
Once we have the features, the tokenized data is then vectorized, with each token receiving a series of vectors, corresponding to each feature extracted during the previous step.

Below is a diagram that illustrates this feature the full vectorization process:

How does a vector database query results?

A vector database's queries are basically just mathematical calculations. Running a query means generating a vector representation of the search query, then comparing this to the vectors values stored for the database's documents. Comparing vectors is done using cosine similarity, which measures the cosine of the angle between two vectors, providing a measure of how similar they are. When comparing vectors, we assume they share a starting point, meaning two vectors always close an angle between 0-180 degrees between each other.

Cosine is a normalization of an angle to a value between -1 and 1, so:

• In case of an angle of 0, meaning identical, the cosine value will be 1.
• In case of an angle of 90, meaning no correlation, cosine will be 0.
• In case of an angle of 180, meaning completely dissimilarity, the cosine will be -1.

Since vectors are both an algebraic, as well as a geometric concept, we can visually represent what this means with a simple diagram. This one shows the cosine similarity of two vectors with the same origin:

What does this mean?
Since vectors represent the tokens' relevancy to the extracted features, the higher the cosine similarity between two vectors, the more relevant they are to each other. By comparing all features between a vectorized input query and the database's documents, we can determine the most relevant results efficiently through mathematical computation.

To understand why this is helpful, imagine an e-commerce site where you can search for "running shoes with good arch support." A full-text search engine might return results that include all the words in your query, such as product listings with the exact phrases "running shoes" or "arch support." However, it might miss relevant products like "athletic sneakers with excellent foot support" because it doesn't understand the semantic meaning behind your query. Consequently, you might end up missing some highly relevant options.

In contrast, a vector search engine will convert your query into numerical vectors that capture its semantic meaning. When you search for "running shoes with good arch support," the engine understands the relevance of the various words in connection with each other. It breaks down both the data and your query word-by-word into vector values, which represent the relevance of words like 'shoe' and 'arch' in relation to each other.

The content within the database has also been vectorized in the same way. For instance, a product described as "performance training shoes with enhanced arches" would be converted into vectors that reflect its similarity to the concept of "running shoes with good arch support." Because both the query and the stored data are analyzed on a word-by-word basis, the connections between related concepts are more easily captured, making it possible for the vector comparison to return relevant results, where no direct word matches would be found otherwise.

By focusing on the meaning rather than exact keyword matches, vector search can return more relevant results. This means natural language queries and nuances can also return relevant results to user search queries.

Where do we go from here?

The explainer up to now has been a primer on vector databases, but how can we use this knowledge for our practical benefits? There are several new vector database platforms available as of the writing of this article. We‘ll explore how they can be implemented and how their results compare to full-text search engines.

Thank you again for sticking around this long! If you like the stuff I write about, buy me a beer! See you in the next article!

Does your company want to use vector search in their applications? Get in touch via my website: https://zatrok.com/